深度学习的数学-卷积神经网络的结构和变量关系
前言
本篇博客主要介绍卷积神经网络的组成部分,以及变量表示,最后附上卷积神经网络代价函数的计算
正文
前文中学到的神经网络都是全连接类型的,隐藏层对输入层有着各自固定的偏好模式,满足偏好模式(权重和偏置来控制)兴奋度会提高; 卷积神经网络在隐藏层也有类似的特性,不过整理偏好的过程是运动的,会将偏好兴奋结果整理到少量神经单元中,以减少神经单元数量,并且可以进行特定的模式识别,可能初看还无法理解这段话,看了下面的过滤器和特征映射应该就会明白了。 本文中所有的例子均为:建立一个神经网络,用于识别 6 * 6 的黑白图像中手写的 1 2 3,那么输入层神经单元就有 6行6列共 36 个
过滤器和特征映射(重点)
过滤器可以理解为一种偏好模式,比如像书中展示的一个过滤器S,对如下形式的图形敏感  那么,拿着这个过滤器,在例子中的 6 * 6 的图形中从左到右,从上到下依次识别,每次识别过滤器S那么大的区域,并将敏感度结果保存起来,相似度越高就越复合过滤器的偏好
那么,拿着这个过滤器,在例子中的 6 * 6 的图形中从左到右,从上到下依次识别,每次识别过滤器S那么大的区域,并将敏感度结果保存起来,相似度越高就越复合过滤器的偏好  得到的结果就是特征映射,也就是根据过滤器S得到的卷积
得到的结果就是特征映射,也就是根据过滤器S得到的卷积 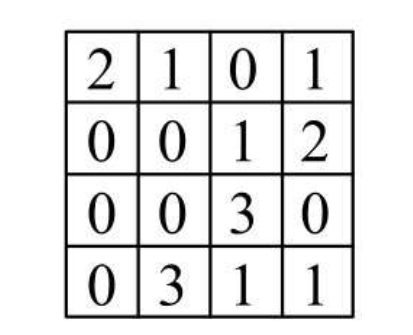
卷积层神经单元输出与池化
简单卷积后,神经单元依旧有 16 个,还是有点多,那么还可以做一个操作叫做池化,书中提到了三种池化方式,首先来看下最简单的最大池化,剩下的两种也很容易理解了 池化的目标就是减少神经单元的数量,但是又能代表卷积层中的结果数据,那么把整个神经单元拆成 2 * 2 的大区域,把每个大区域的最大值(最大输出)作为代表放到池化层的对应位置,即可得到池化的结果 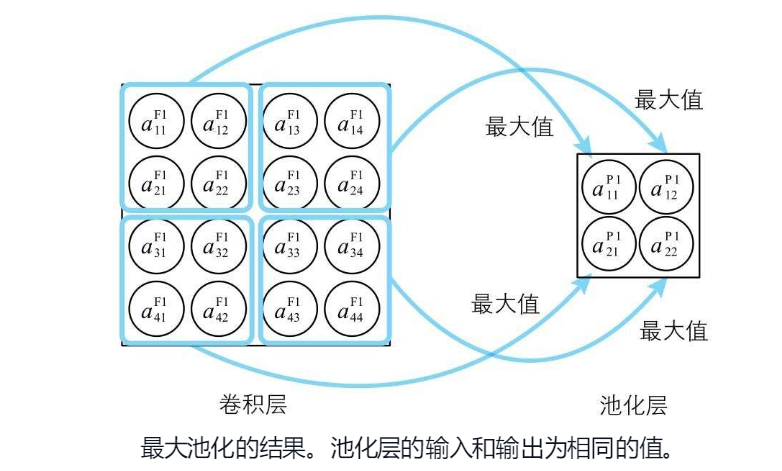
三种池化方式
书中提到了如下三种池化方式:
- 最大池化,使用区域中最大值作为代表值
- 平均池化,使用区域中的平均值作为代表值
- L2池化,使用平方和开方的值作为代表值,$\sqrt{a_1^2+a_2^2+a_3^2+a_4^2}$
变量和参数定义(重点)
书中给到了如下参数定义,结合第二幅图可能更能够理解 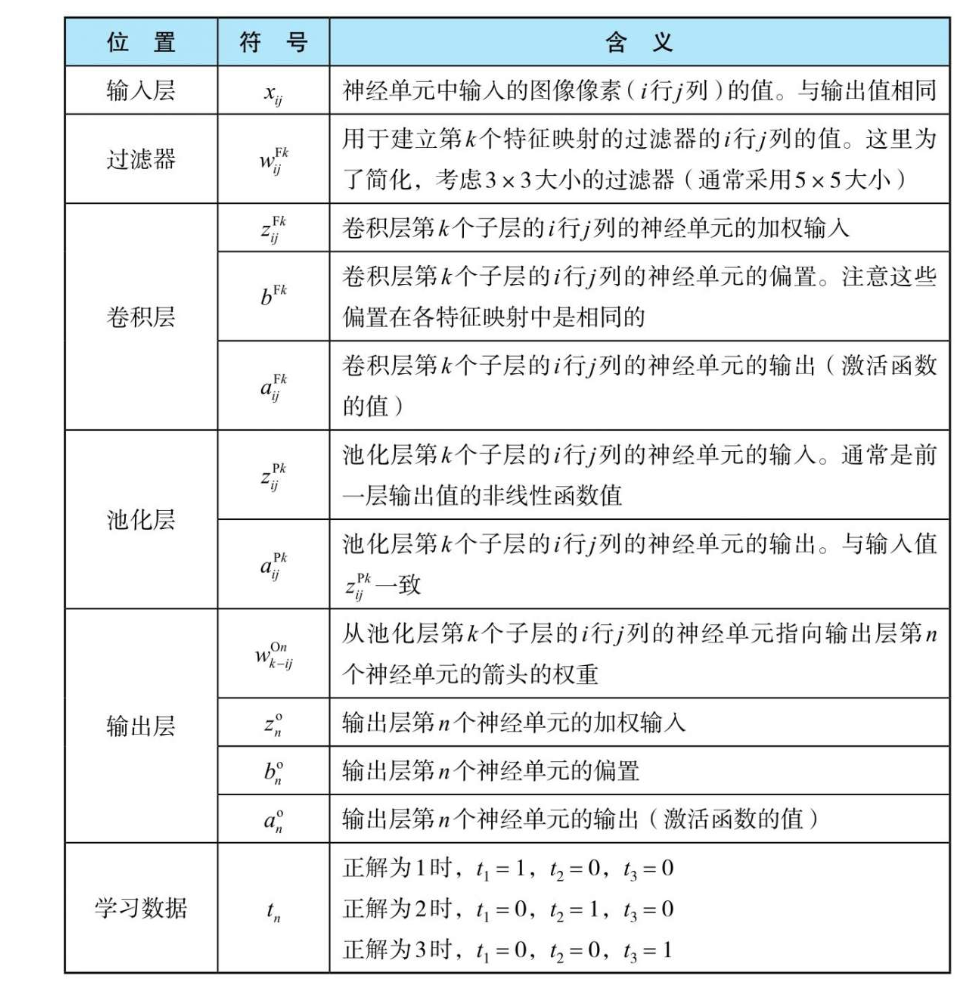 简单地说,输入层右上角带上了 I 表示Input,每个过滤器K对应了以 $w_{ij}^{Fk}$ 表示的神经单元,经过过滤器的卷积计算都对应生成的结果(特征映射结果),卷积层中的加权输入依旧用z表示、偏置用b表示、输出用a表示,不过右上角的F代表Filter;卷积层对应的池化层也是如此,但是池化层的神经单元输出等于输入,所以没有偏置;输出层的变化是,右上角带上了一个O,表示Output,学习数据与之前的别无二致
简单地说,输入层右上角带上了 I 表示Input,每个过滤器K对应了以 $w_{ij}^{Fk}$ 表示的神经单元,经过过滤器的卷积计算都对应生成的结果(特征映射结果),卷积层中的加权输入依旧用z表示、偏置用b表示、输出用a表示,不过右上角的F代表Filter;卷积层对应的池化层也是如此,但是池化层的神经单元输出等于输入,所以没有偏置;输出层的变化是,右上角带上了一个O,表示Output,学习数据与之前的别无二致 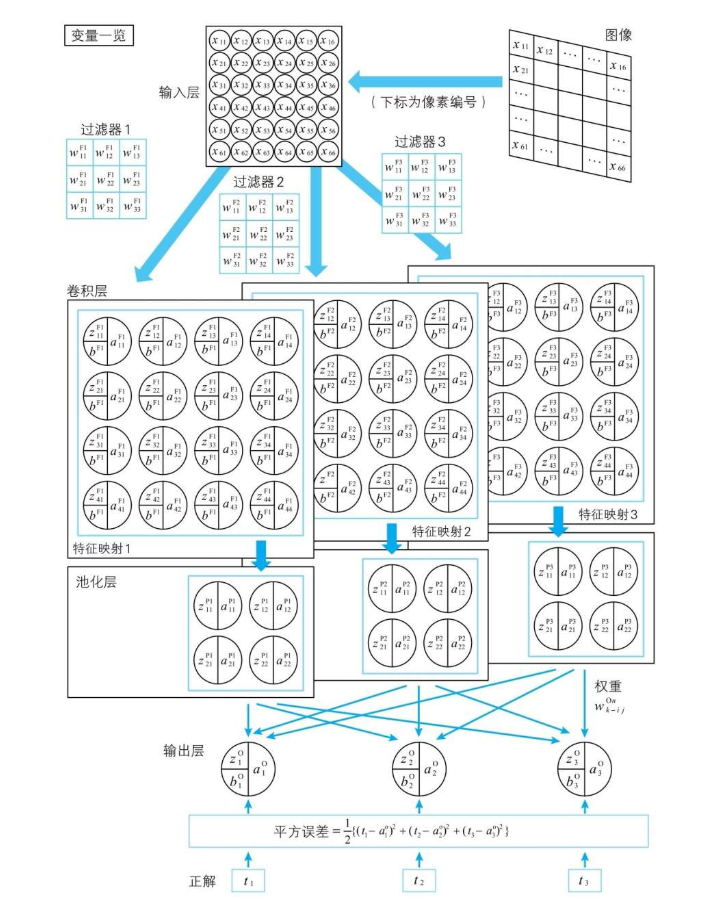
各个层的变量关系
输入层
输入层中的神经单元,输入等于输出,所以 $a_{ij}^I = x_{ij}$
过滤器和卷积层
过滤器,右上角的F代表 Filter,过滤器中的w同样代表了对应位置的神经单元与过滤器中神经单元的权重 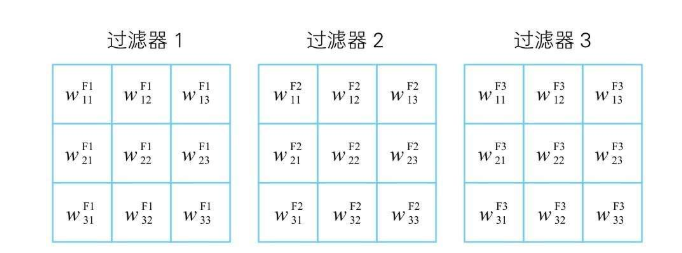 所以第一块区域使用第一个过滤器得到的卷积结果 $c_{11}^{F1}=w_{11}^{F1}x_{11}+w_{12}^{F1}x_{12}+w_{13}^{F1}x_{13}….w_{33}^{F1}x_{33}$
所以第一块区域使用第一个过滤器得到的卷积结果 $c_{11}^{F1}=w_{11}^{F1}x_{11}+w_{12}^{F1}x_{12}+w_{13}^{F1}x_{13}….w_{33}^{F1}x_{33}$  不难得到一个 3 * 3 的过滤器,卷积结果公式如下,如果不是 3 * 3,w的最终下标再变化下即可
不难得到一个 3 * 3 的过滤器,卷积结果公式如下,如果不是 3 * 3,w的最终下标再变化下即可 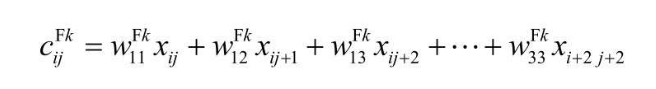 一般的,过滤器会有自己的偏置 $b^{Fk}$,这个偏置与输入层的神经单元无关,与过滤器中的神经单元也无关,最终得到如下的加权输入(输入到特征映射-卷积层神经单元)
一般的,过滤器会有自己的偏置 $b^{Fk}$,这个偏置与输入层的神经单元无关,与过滤器中的神经单元也无关,最终得到如下的加权输入(输入到特征映射-卷积层神经单元) 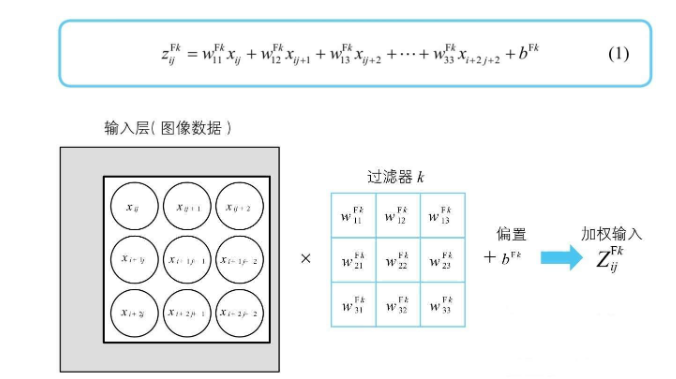 卷积层的神经单元激活函数用 a 表示,所以卷积层的神经单元可以如下图表示
卷积层的神经单元激活函数用 a 表示,所以卷积层的神经单元可以如下图表示 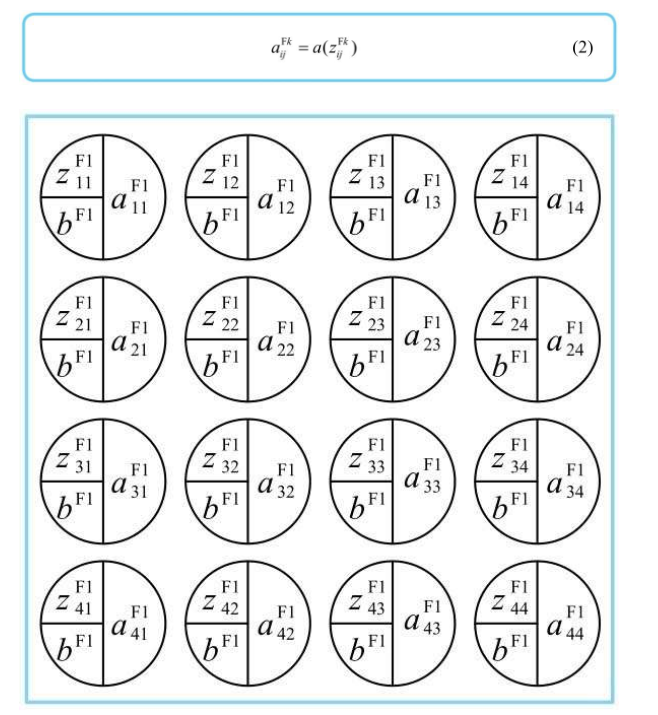
池化层
就是把卷积层的神经单元结果压缩到更少的神经单元中 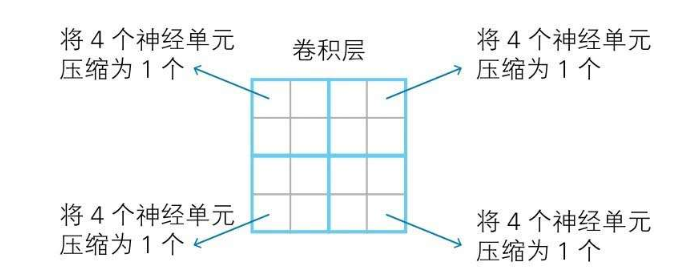 最大池化,就简单求一下几个神经元输出的最大值就可以了
最大池化,就简单求一下几个神经元输出的最大值就可以了 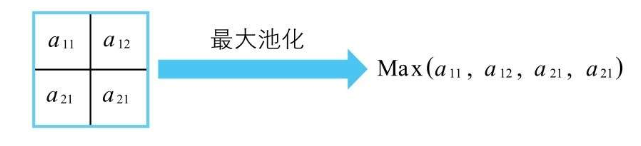 然后池化层的神经单元,输入等于输出,激活函数 $a(x)=x$
然后池化层的神经单元,输入等于输出,激活函数 $a(x)=x$ 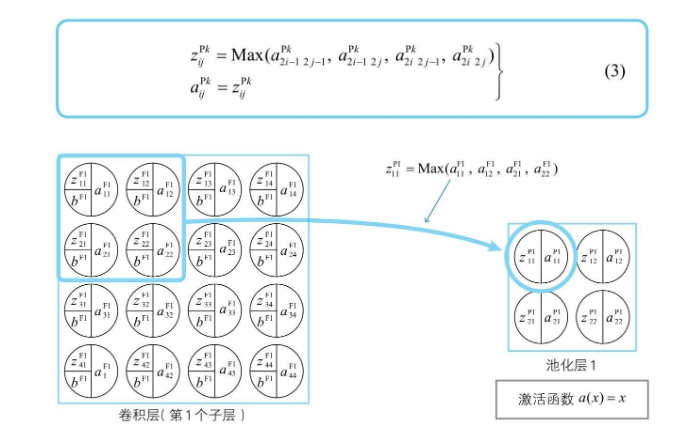
输出层
池化层和输出层的连接方式为全连接,输出层神经单元的输入就是权重求和,再加上池化层的整体偏置即可 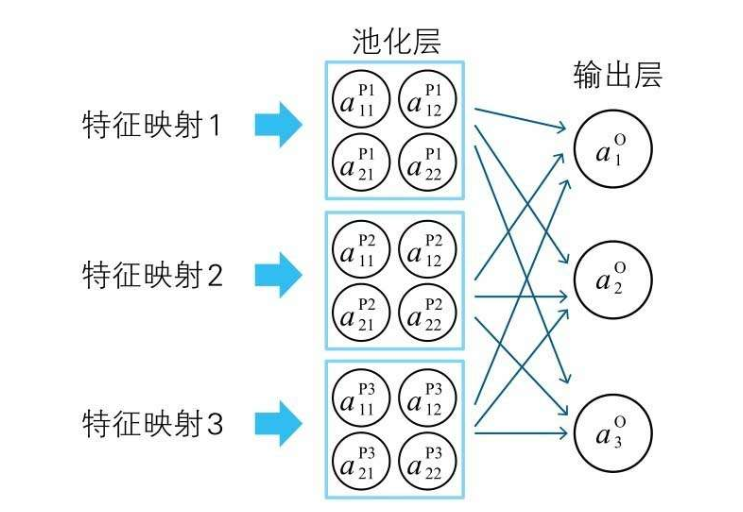 不难得到如下式子
不难得到如下式子  最后激活函数处理下,就可以得到输出神经单元的输出值
最后激活函数处理下,就可以得到输出神经单元的输出值 
代价函数的计算
上面拿到输出神经单元的输出值后,根据代价函数的定义,把正解和输出值做差值平方即可得到平方误差C  与之前全连接层的式子类似
与之前全连接层的式子类似 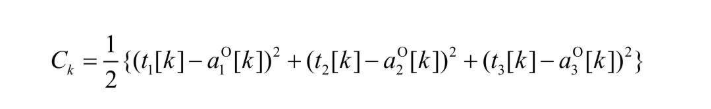 经过多次学习,得到多个平方误差C,那么整个神经网络的代价函数就可以表示为如下式子
经过多次学习,得到多个平方误差C,那么整个神经网络的代价函数就可以表示为如下式子 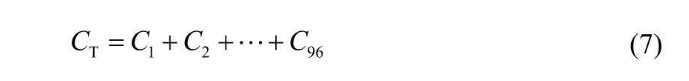 同样的,需要像之前一样得到代价函数在最小值的时候的各个参数(各个神经单元的偏置和权重),同样可以使用误差反向传播计算梯度,再通过梯度下降推导各个参数的最优解。
同样的,需要像之前一样得到代价函数在最小值的时候的各个参数(各个神经单元的偏置和权重),同样可以使用误差反向传播计算梯度,再通过梯度下降推导各个参数的最优解。
总结
主要介绍了过滤器、卷积层和池化层中间的关系和工作原理,以及在卷积神经网络中各个层的变量参数定义,以及各个层之间的数学关系,最后得到了代价函数。