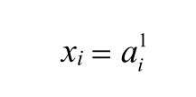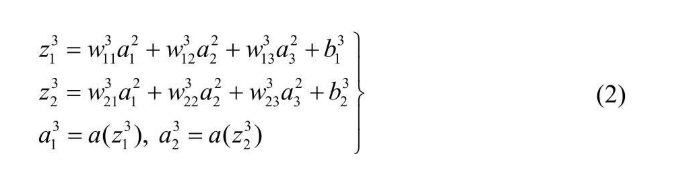
深度学习的数学-神经网络关系式、代价函数最优化
前言
本篇博客主要讲解神经网络中的变量表示法、各层的输入输出关系式,了解正解和预测值,代价函数的计算及其最小化,以及参数规模和需要的数据规模计算
正文
神经网络的参数表示法
据书中表述,神经网络是一种数学模型,像权重和偏置在数学上看就是参数 下图中,权重 w1/w2/w3 偏置 b 就是神经单元的参数,加权输入即为z1,经过激活函数 a 的计算得到结果为 a1 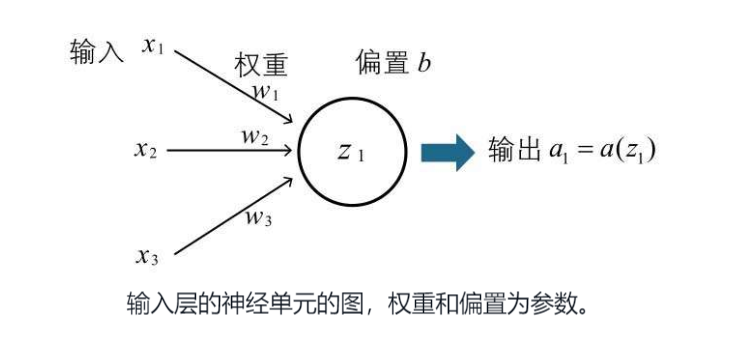
命名规则(重点)
上面简单看了下一个神经单元的输入输出表示,但是神经网络由多个层组成,每个层又有多个神经单元,所以需要科学的对这些神经单元编号
层编号
首先,对神经网络的每个层进行编号,从输入层开始数,输入层为层1,输出层为最后一层,也就是 层l,l表示 last 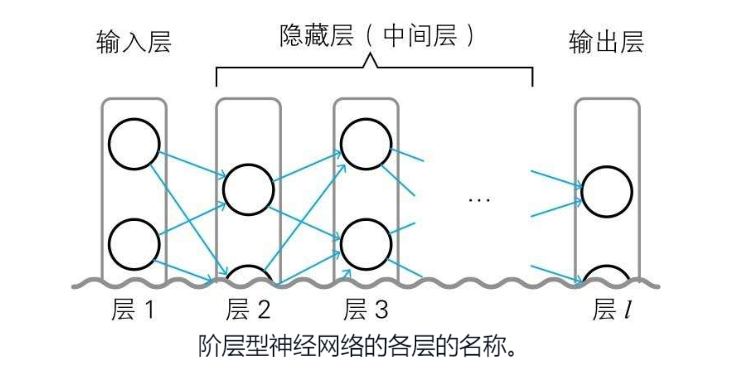 然后每个层对应的偏置和权重,有如下的规则定义
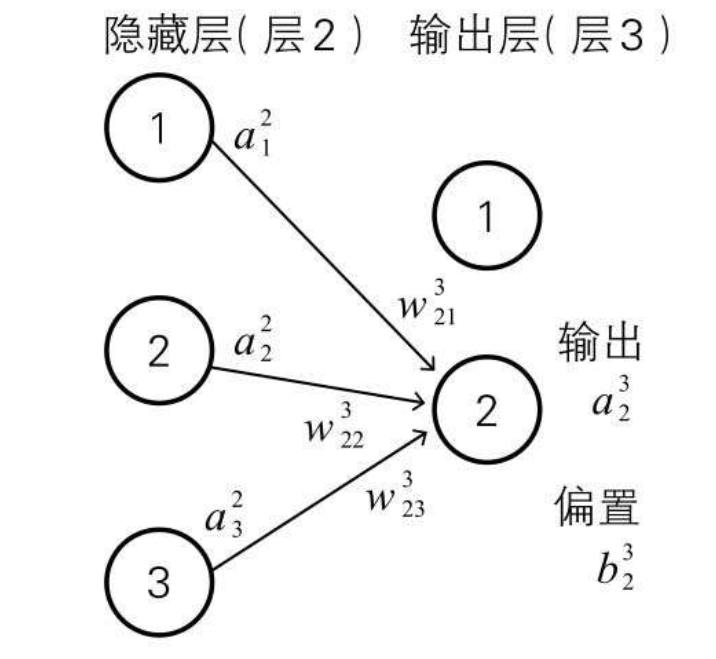
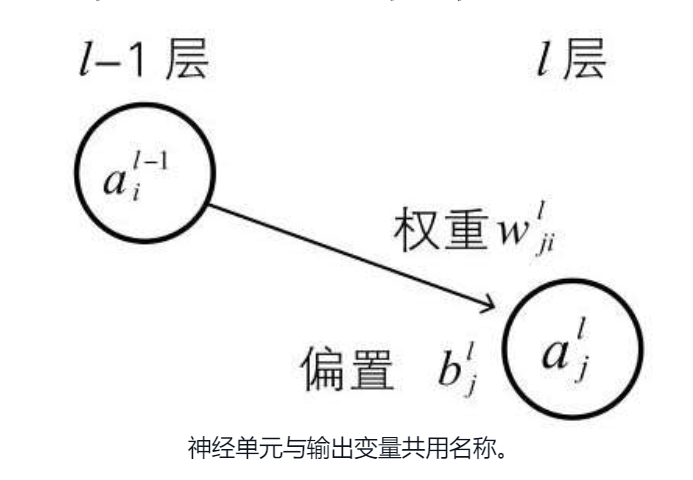
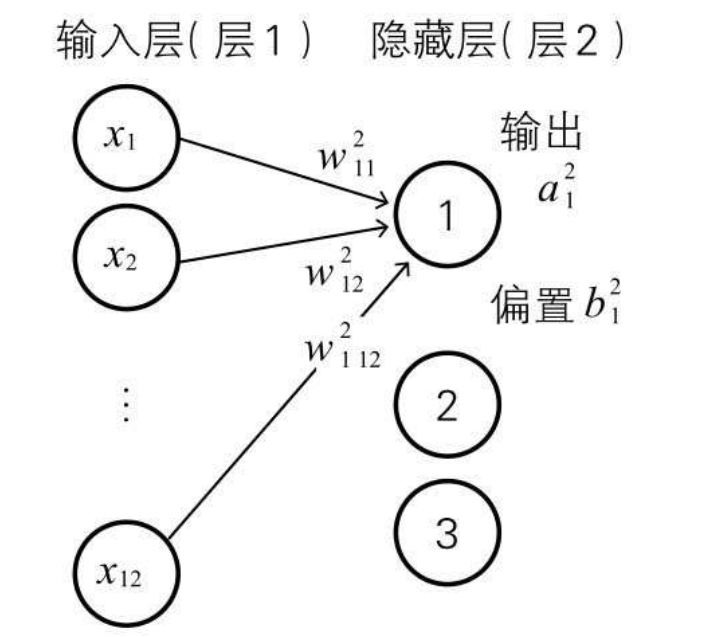
然后每个层对应的偏置和权重,有如下的规则定义 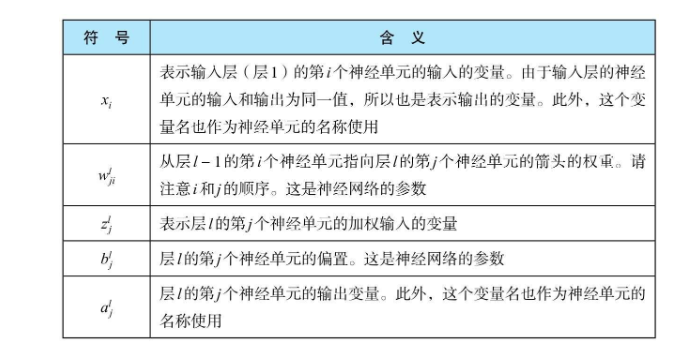 看表格可能有点难理解,可以参照下图的表现形式,需要着重理解权重(w)的下标有两个索引,前面的索引代表当前层的第几个神经单元,后边的索引代表前一层输出的第几个神经单元
看表格可能有点难理解,可以参照下图的表现形式,需要着重理解权重(w)的下标有两个索引,前面的索引代表当前层的第几个神经单元,后边的索引代表前一层输出的第几个神经单元 
 下面是截取的一个 3*4 的黑白图像识别神经网络,输入层隐藏层和输出层的命名表示
下面是截取的一个 3*4 的黑白图像识别神经网络,输入层隐藏层和输出层的命名表示 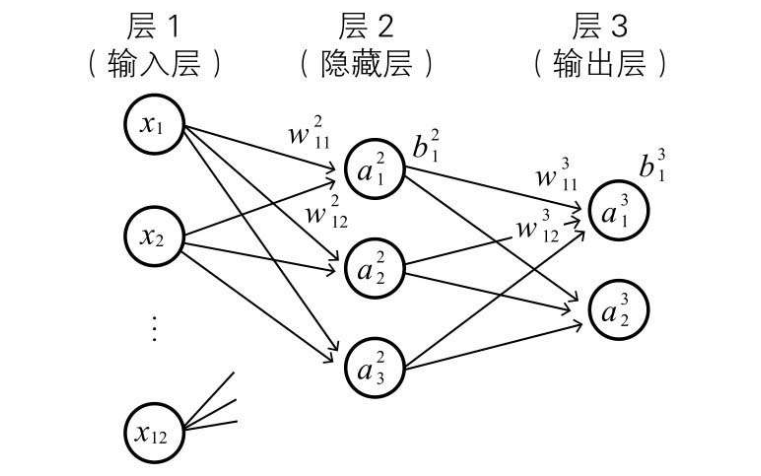
小练习
这是博主自己编的几个小练习,可以对照下表格第一列理解其输出含义
符号
表示含义
${w_{11}}^{2}$
第1层第1个神经单元对应第2层第1个神经单元输出权重
${w_{21}}^{2}$
第1层第1个神经单元对应第2层第2个神经单元输出权重
${w_{21}}^{3}$
第2层第1个神经单元对应第3层第2个神经单元输出权重
${x_{12}}$
第一层(输入层)的第十二个神经单元名称 或 输入 或 输出变量
${z_{2}}^{3}$
第3层第2个神经单元加权输入的变量
${b_{2}}^{3}$
第3层第2个神经单元的偏置
${a_{2}}^{3}$
第3层第2个神经单元的输出变量 或 表示该神经单元的名称
多个学习实例的表示方法
可以加上中括号来表示第n个学习实例  下图表示第七个图像输入神经网络时,对应的变量表示方法
下图表示第七个图像输入神经网络时,对应的变量表示方法 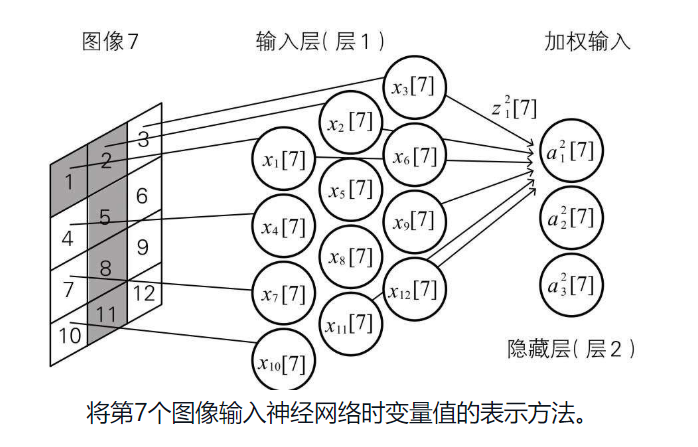
关系式
关系式就是用一个式子表示各个变量之间的关系
输入层
隐藏层(中间层)
根据变量的定义,不难得出如下的关系式(z和a定义请见本博客上方表格) 
输出层
矩阵表示法
之前理解过矩阵内积的相关知识,权重之和 z 可以用如下的向量形式表示,有利于编程的实现 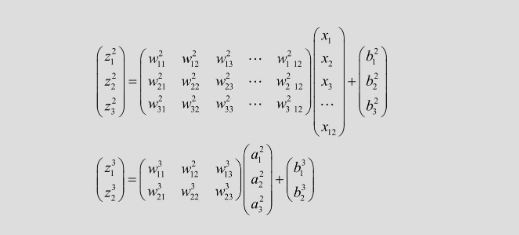
正解和代价函数
正解的定义
正解顾名思义就是学习数据中正确的结果,预测值就是输入模型产生出来的结果值 用事先提供的学习数据确认权重和偏置,这个过程在神经网络中被称作学习,目标就是让预测值与正解的误差尽可能的小 如下图所示的识别 3*4 的黑白图像是0还是1,输出层 ${a_{1}}^{3}$ 敏感度越高,越偏向1,反之结果越偏向0 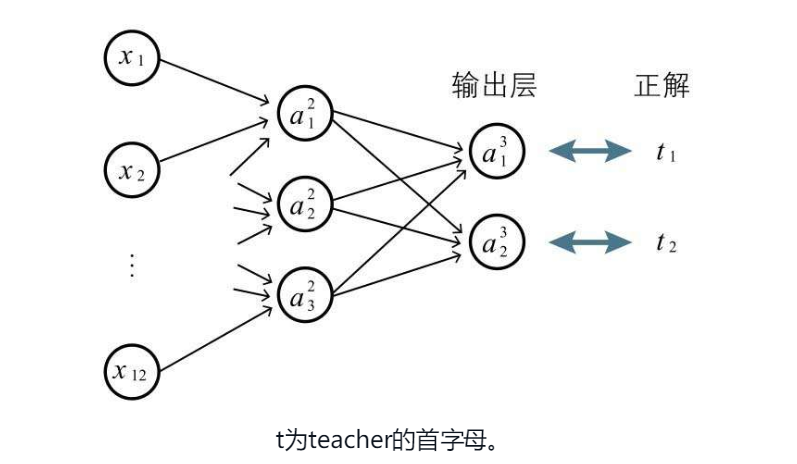 如果我们得到的学习数据是一张图片对应一个数字 1或0,那么还需要画出表格做出如下定义 实际的学习过程就如下图所示,根据正解和输出层的结果,就可以求误差了
如果我们得到的学习数据是一张图片对应一个数字 1或0,那么还需要画出表格做出如下定义 实际的学习过程就如下图所示,根据正解和输出层的结果,就可以求误差了 
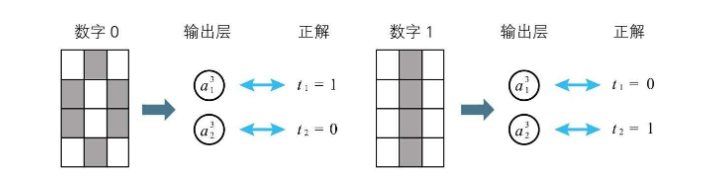
代价函数
这里引入书中的一段话来表示代价函数,大概意思就是衡量这个模型的误差大小的一个函数
在数学中,用模型参数表示的总体误差的函数称为代价函数,此外也可以称为损失函数、目的函数、误差函数等。如前所述(2-12节),本书采用“代价函数”这个名称。
代价函数的计算
代价函数也分很多种,比如最容易理解的每一个学习数据的(正解 - 预测值) ^ 2 之和 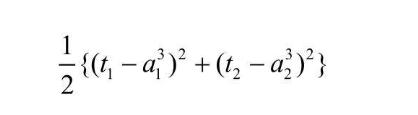
书中说明了,1/2 作为常数是为了方便计算
由于对差求平方的代价函数虽然很容易理解,但是存在着计算收敛时间长的问题,为解决这个难点,书中还提到了另外一种误差指标,称为交叉熵,提高梯度下降算法的速度 针对本博客上方的两个输出神经单元的例子,定义如下,其中 n 是数据的规模 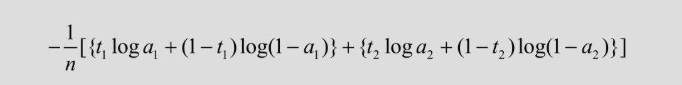
代价函数的最小化(重点)
书中给到了如下一张比较容易理解的图,因为代价函数的式子直接体现模型的误差,所以只需要让代价函数尽量小,整个模型契合度就会越高  那么如何让代价函数最小呢,不知道有没有想到之前提到的 多变量函数求极值 的问题,多变量函数的极值有一个必要条件,就是 对每个变量求偏导数,其值均为0 具体可以见之前写过的一篇博客 深度学习的数学-导数和偏导数 但是在实际的训练过程中,求导数的计算量比较大,更多是采用梯度下降的方式去求极值 之前也写了相关博客可供参考 深度学习的数学-梯度下降
那么如何让代价函数最小呢,不知道有没有想到之前提到的 多变量函数求极值 的问题,多变量函数的极值有一个必要条件,就是 对每个变量求偏导数,其值均为0 具体可以见之前写过的一篇博客 深度学习的数学-导数和偏导数 但是在实际的训练过程中,求导数的计算量比较大,更多是采用梯度下降的方式去求极值 之前也写了相关博客可供参考 深度学习的数学-梯度下降
神经网络的代价函数
还是以 3*4 图片识别0/1的神经网络为例 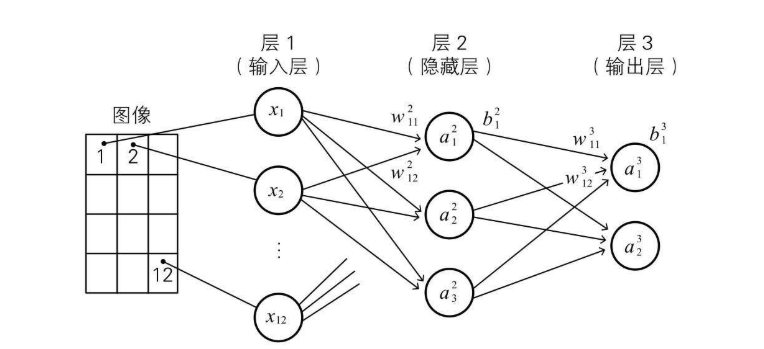 假设有64张图片,则其误差可以表示如下
假设有64张图片,则其误差可以表示如下 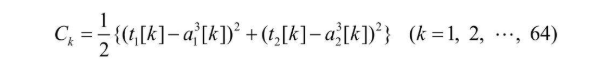 然后把每张图片(学习资料)的误差加起来,就得到了代价函数
然后把每张图片(学习资料)的误差加起来,就得到了代价函数 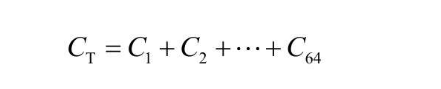
参数和数据规模的计算(重点)
书中提到了参数规模的最小值估算方法,就是把所有的权重、偏置都数起来,因为这些都是需要通过学习资料去确定的参数  书中提到,数据的规模如果小于参数的规模,就无法确认模型,所以最小数据规模就是所有参数的个数,3*2图像的那个例子学习用的图像至少需要47张
书中提到,数据的规模如果小于参数的规模,就无法确认模型,所以最小数据规模就是所有参数的个数,3*2图像的那个例子学习用的图像至少需要47张
总结
本篇主要记录神经网络的参数表示法,每个层每个神经单元的关系式,正解和代价函数,以及代价函数最小化、参数和训练数据规模等