深度学习的数学-数列递推和Σ

2020年02月26日机器学习约1k字预计需要4分钟

前言

本篇博客主要复习下高中数学中的数列，包括数列的三种表示形式，一种是通项公式，另一种是递推关系式，另一种是联立递推关系式神经单元的输入计算就涉及到这种递推式；另外还介绍了Σ运算的规则及常用形式。

正文

数列基本概念

数列是数的序列，比如如下偶数数列

2,4,6,8,10

其中第一个数称为首项，第二个数称为第2项，第三个数称为第3项，第n个数称为第n项 如果一个数列是有限项的，那么这个数列被称为有穷数列，有穷数列中，最后一项被称为末项

数列的通项公式

在数列的表示中，一般用 a1表示首项，a2表示第2项，an表示第n项，那么如果有一个式子能将 an 用关于 n 的式子表示出来，那么数列的每一个值就都能得到确定，那么这个式子就叫做数列的通项公式 比如，通项公式 an = 2n，那么把 n 从 1 到 n 带入进去，就会得到如下数列

2, 4, 6, 8, …

比如我们得到了如下数列：

1,3,5,7,9, …

也很容易就能推断出其通项公式为 an = 2*n-1

数列的递推关系式

数列也可以用相邻项来表示，举个最常见的例子，也就是著名的斐波拉契数列，有个特征就是当n>2时，第n项等于第n-1项及n-2项之和

1,1,2,3,5,8,13,21,34,55,89,144,…..

当n = 1或n=2时，数列值为0，当 n > 2 时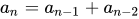，用递推关系式表达这个数列很简单也很容易理解，但如果要用通项公式就会是下图这个样子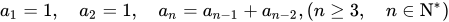：具体推导方法不做具体介绍，详情可参考百科：https://baike.baidu.com/item/%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97/99145?fromtitle=%E6%96%90%E6%B3%A2%E6%8B%89%E5%A5%91%E6%95%B0%E5%88%97&fromid=10078434&fr=aladdin 计算机比较擅长递推公式的计算，比如斐波拉契序列在 python 中就可以很快速的实现

1
2
3

arr = [1, 1]
for i in range(2, 12):
    arr.append(a[i - 1] + a[i - 2])

数列的联立递推关系式

参考下书中的例题，其中 a1 = b1 = 1 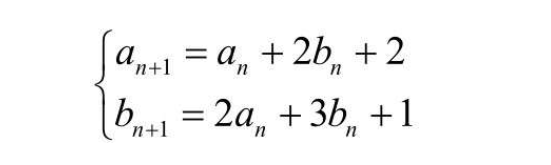可以推导出 a2 = a1 + 2*b1 + 2 = 5;b2 = 2*a1 + 3*b1 + 1 = 6;..... 得到两个数列：

a = 1, 5, 19, … b = 1, 6, 29, …

这就是联立递推式，在程序中也比较好实现

a = [1]
b = [1]
for i in range(1, 12):
    a.append(a[i-1] + 2*b[i-1] + 2)
    b.append(2*a[i-1] + 3*b[i-1] + 1)
print(a, b)

联立递推式在神经网络中的应用

a(l,j) 表示第l层，第j个神经单元 w(l,jk) 表示第l层，第j个神经元对应上一层第k个神经元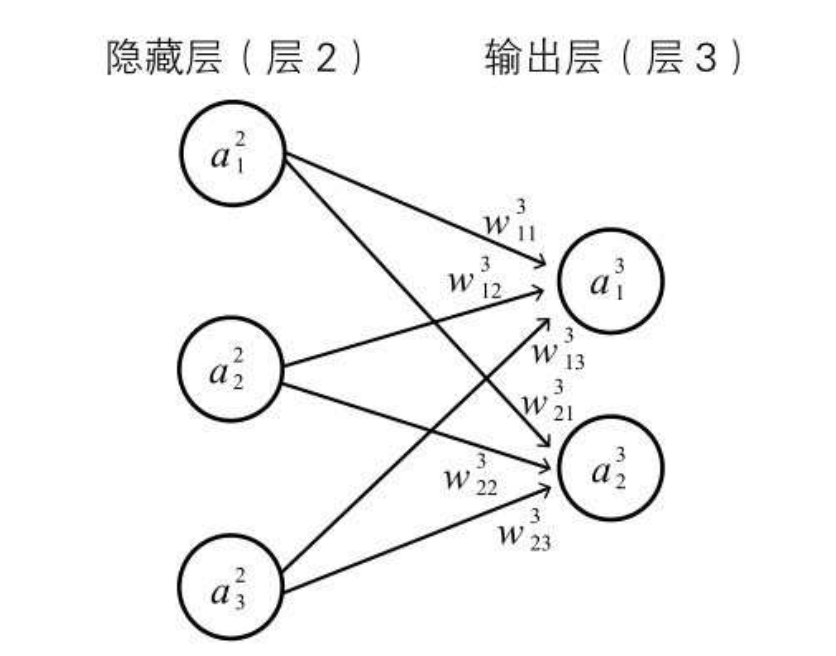以隐藏层到输出层的神经单元信息传递为例，其规则满足如下递推式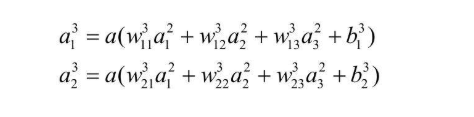

Σ符号的含义

Σ读作Sigma，表示求和比如我想对数列 {an} 的首项到第n项求和，那么可以表示为其中Σ下方的k=1表示初始值，上方的n表示最终值，右侧的带k的表达式（如：ak），表示取数列中的哪一项

Σ的几种常见用法

比如，求数列 a1 + a2 + a3 + a4 + a5 可以这样表示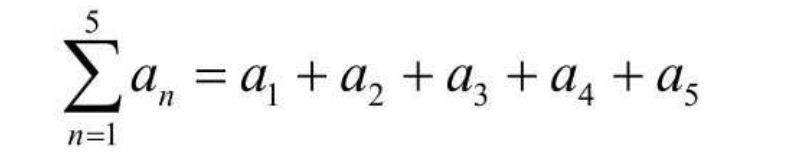：求 1^2 + 2^2 + 3^2 + 4^2 + 5^2 + 6^2 + 7^2，可以这样表示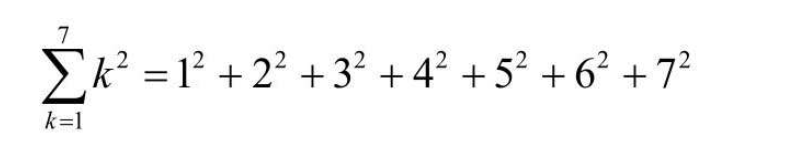：求 2^1 + 2^2 + … 2^m，可以这样表示

Σ的几个性质及证明

Σ具有线性性质，比如 Σ(ak + bk) = Σ(ak) + Σ(bk),Σ(c*a) = c*Σ(a) 证明过程如下，挺好看懂的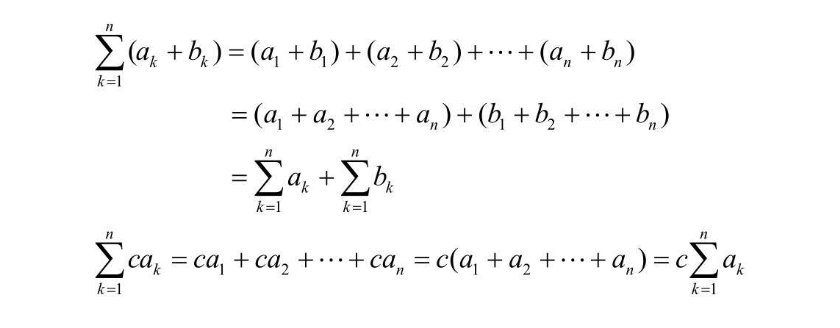

总结

本篇主要介绍数列相关内容，包括其通项公式表示法、递推表示法、联立递推表示法（重点）；以及Σ的定义、常见用法及性质。