算法基础-散列表的原理及基础操作
前言
本篇博客主要分享数据结构中关于散列表的定义和编程实现
正文
什么是散列表
散列表也成为Hash表,用于存储 Key 和 Value 的集合,对于某一个Key,散列表能以接近O(1)的时间复杂度获取到对应的value
Hash的数据结构
散列表读取的时间复杂度能达到 O(1),这与其结构脱不了干系 学过基础数据结构都应该知道,通过数组的索引进行顺序读写时间复杂度就是O(1),那么Hash就借用了这一特点 在进行数据存储或者读取的时候,首先通过散列函数计算出Key这个字符串对应的数字,简单取模,得到 0~当前数组长度的一个索引,根据索引顺序存取,时间复杂度就是O(n)
存储数据的数组
散列函数
Hash的负载因子
负载因子用于表示Hash的空间使用程度,计算公式为 Hash有效数据长度/数组长度(空间) 负载因子越高,Hash的查找效率可能就会收到影响,因为负载因子越高就越容易出现Hash冲突,无论是开放寻址法还是链表法都会让查找速度降低 一般在负载因子达到一定限制的时候,Hash就需要自动扩容,以保证足够的查找性能
开放寻址法
当Hash冲突的时候,存放元素的时候往后移至空位,查找到对应索引时如果当前索引已经存在元素,那么就往后找到一个空白的位置放入 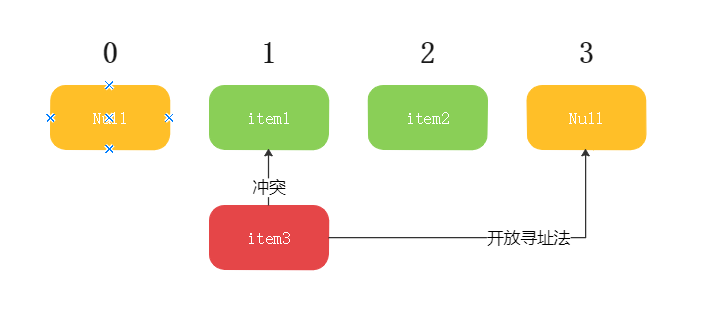
链表法
当Hash冲突后,存放元素的item中的链表指针域往后追加新的元素 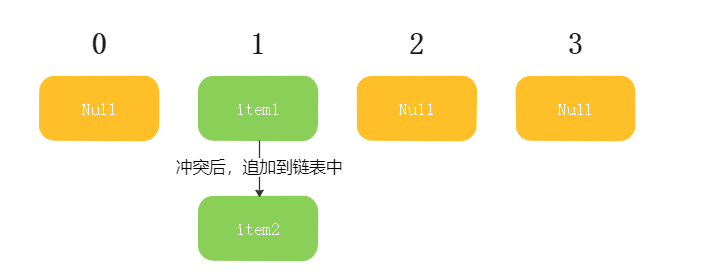
Hash结构的几个操作
读操作
开放寻址法的读操作
开放寻址法中,由于冲突时元素向后查找空位,所以查找的时候需要判断查找的key和存储的key是否相同,不相同的时候需要向后查找相同key的元素,直到为空或者找到相同key的元素 
链表法的读操作
链表法中,冲突元素直接挂在Hash数组的指针域中,所以查找的时候,首先判断查找的key和存储在数组中的key是否相同,不相同的时候需要在指针域对应的链表中查找(时间复杂度O(N)) 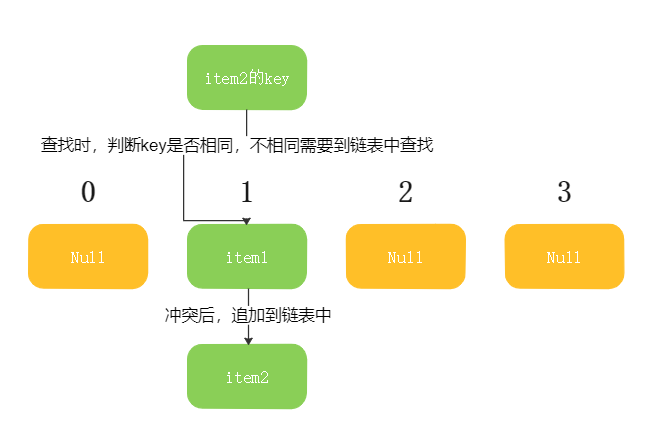
写操作
开放寻址法的写操作
先使用散列函数计算key对应的索引,如果冲突,则往后查找到一个非空的位置写入 
链表法的写入
散列计算key对应的索引,如果冲突,追加到数组元素中的链表域
扩容
无论是开放寻址法还是链表法,扩容都需要新建一个哈希表,重新计算Hash值之后返回新的哈希表 负载因子过小的时候也可以触发收缩,重新计算所有元素的Hash值,以节省空间 
总结
本篇介绍了Hash表的数据结构基础,以及两种解决Hash冲突的策略,以及对应策略的读取、写入、扩容操作的底层操作